等差数列の和 公式 証明 616640-等差数列の和 公式 証明

 初項が a a a ，末項が l l l ，項数が n n n であるような等差数列の和は， 1 2 n (a l) \dfrac{1}{2}n(al) 2 1 n (a l) →等差数列の和の公式の例題と証明など 等比数列 例： 1 2 4 8 16 = 31 =31 1 2 4 8 16 = 31 初項が a a a ，公比 r r r ，項数 n n n の等比数列の和は（ r ≠ 1 r\neq 1 r = 1 のもとで）， 数bの等差数列の性質の証明問題です。 p、qが定数のとき、一般項がan=pnqで表される数列｛an｝は等差数列であることを示せ。 この問題の解答に an=pnqからan1=p(n1)q ということが書 かれていました。そもそも，等比数列と言えるためには，比が一定の「定数」，すなわち「項の番号に依存しない定数」として「どの2項間にも共通の定数」でなければならないのに， というように n に応じて変化していくような比率になっていると等比数列ではなく，その和の公式も使えません．

階差数列

等差数列の和 公式 証明

等差数列の和 公式 証明-MathAquarium定理・公式の証明数列の公式 1 1 等差数列 等差数列{a n}の初項をa，公差をd，末項をl，一般項をa n，初項から第n 項までの和をS n とすると a n＝a＋(n－1)d， S n＝ 2 1 n(a＋l)＝ 2 1 n{2a＋(n－1)d} 2 等比数列 等比数列{a n}の初項をa，公比をr，一般項をa等差数列の和の公式 (A) 初項 a ，末項 l ，項数 n の等差数列の初項から末項までの和 S n は (B) 初項 a ，公差 d ，項数 n の等差数列の初項から第n項までの和 S n は ※どちらも アン（ a, n ）は必須 デル（ d, l ）は1つ選びます．

数学b 等差数列と等比数列 Mike先生のstudyブログ

 POINT 1 等差数列の和は ひっくり返して足す 。 2 n個だけ 同じ数字が現れる。 3 なので、 最後に2で割るのを忘れない！ 以上となります。 等差数列の解説から来た人は、そちらへ戻りましょう〜！ 等差数列一般項や等差数列の和の証明 等差数列の3 等差数列 次のような数列 {a n} 1, 4, 7, 10, 13, 16, 19, 22, 練習問題2 等差数列をなす 3 数がある。その和は 15 で，平方の和は であるという。 等差数列のときと似たような導入でかきます。覚えなくていい「等差数列の和」 算数は得意なのに数学が苦手なひとのためのブログまず、等比数列の公式として、 こんな感じで教わってるかな？ それとも みたいな感じ？ こんな感じで覚えてると、は？

等差数列の公式は？3分でわかる公式、覚え方、等差数列の和の計算 7/1最新版入荷！一級建築士対策も ！290名以上の方に大好評の用語集はこちら⇒ 全92頁！ 収録用語1100以上！ 等差数列に関しては公式を使って和を求めたなぁ〜という淡い記憶しか持ち合わせていません。 そもそも私のような数学音痴は、公式を覚えてからその証明を覚える。ひたすら暗記なわけです。しかも覚えるの公式 → 証明の順。等差数列の和の公式 S n =1/2n(al) 等差数列を利用する倍数の和;

 高2 等差数列の和の公式の証明 高校生 数学のノート Clear 表紙 1 公開日時 年08月28日 19時53分 更新日時 年08月28日 19時57分 こんにちは。 da Vinch (@mathsouko_vinch)です。 数列の和にはどんな情報があるのか数列の和は数列のそれぞれの項の和でした。 等差数列や等比数列など、特徴が顕著に現れる数列では和の公式を考えて簡単に求めることができよって，2S10=24×10=240 より S10=1 となります。 一般に，初項 a，公差 d，項数 n の等差数列の末項を としますと，初項から第 n 項までの和 Sn は， Sn=a (ad) (a2d) (d) (3) となります。 また，S10は上の例と同様に， Sn= (d) (2d) (ad)a (4) と書けますので， (3)と (4)の辺々加えますと，

みんなの算数オンライン 教科書 等差数列の和

一次関数 の新着タグ記事一覧 Note つくる つながる とどける

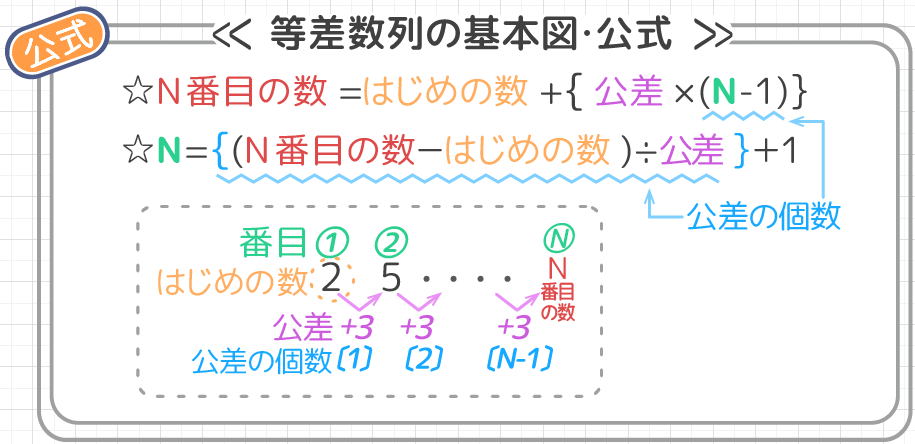
陈金跃 等差数列求和公式的变换与意义j 中学数学研究, 02(12)4142 3 刘锡凤 等差数列求和公式的应用教学设计j 中国科教创新导刊, 13(2)9495 4 齐龙新, 王红艳 等差数列求和公式变式的灵活应用j 高中数理化, 09(2) 5 杜莹梅 等差数列求和公式的 階差数列を用いて一般項を求める公式の証明 の階差数列 は の隣り合う2項の差なので、 は2項以上存在していないと を定義することができません。 よって、 (1) である必要があります。 に を代入すると、 上式を全て足すと、 よって最終的に等差数列の和公式は以下のようになります。 S n = n (a 1 a n) 2 この式から等差数列の和は最初の項 a 1 と最後の項 a n だけわかれば計算することができることがわかります。

1乗和 2乗和 3乗和の公式 導出法から理解しよう

高校数学b 適当に並び替えると等差数列にも等比数列にもなる3数 受験の月

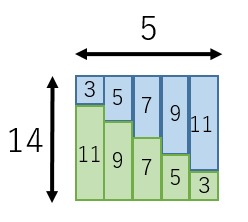
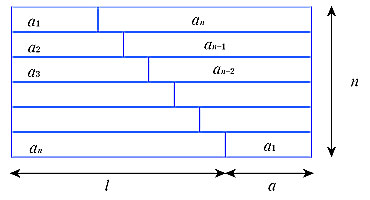
 二乗の和の公式の証明 まずは二乗から考えていきましょう。 そもそもどんな和を考えるのだったかというと ∑ k = 1 n k 2 = 1 2 2 2 3 2 n 2 でした。 考えることは『二乗の和が出てくるような上手い形の式がないか』です。 ここで見るべきなのは次話をもとに戻して，等差数列の和の公式も上の台形の図と同様の図で説明できることを示そう． まず，数 x を（正の数に限るが） x cm の長さのテープとして表そう．そうすると，数列（数の並び）はテープの並びとして表される． 例えば， 等差数列の和を求める公式 等差数列の初項からある項までをすべて足し合わせる公式がある。 初項a、末項l、項数nの等差数列の和S n を求める公式は以下。 この公式についても具体的な数列を使いながら証明していきたい。 ＜公式の証明＞

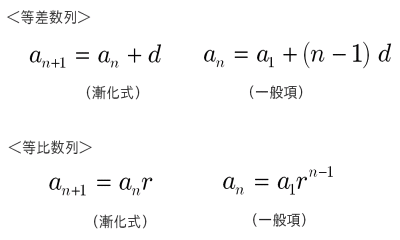
数列 漸化式と一般項 大人が学び直す数学

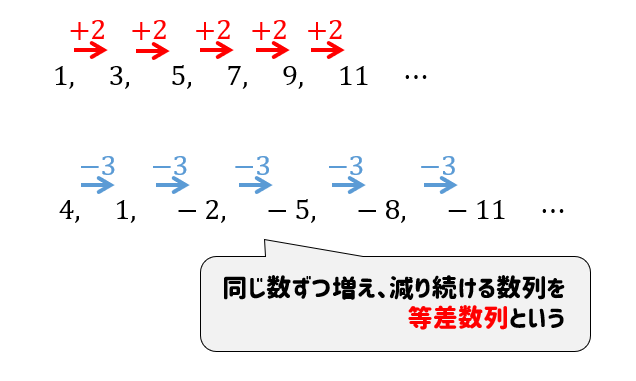
等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

 ここで図の赤枠で示している部分に注目してください。この部分は等差数列になっています。ですので、等差数列の 番までの和の公式を使って求めることができます。 そして出てきた値に初項を足すと 1＋45＝46となります。 答え46 まとめ等差数列の和の公式導出 公式の導出 等差数列 {a n} の初項を a 1 ，公差を d とすると， a 2 = a 1 d a 3 = a 2 d = a 1 2 d a 4 = a 3 d = a 1 3 d a 5 = a 4 d = a 1 4 d , ⋅ ⋅ ⋅ よって，第 n 項は， a n = a n − 1 d = a 1 (n − 1) d また，第 n 項までの和は， S n = a 1 等差数列的前n项和公式与函数的关系给出了一种判断数列是 否为等差数列的方法：若数列{an }的前n项和S =an^2bnc，那 么当且仅当c = 0时，数列{an }是以a b为首项， 2a为公差的等差 数列；当c ≠ 0时，数列{an} 不是等差数列。 2、求解等差数列的通项及前n项和

48s96ub7b0z5f Net Tousa Suuretsu

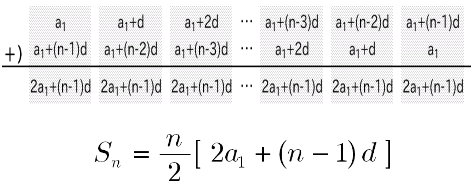
数列 等差数列の和を求める 大人が学び直す数学

You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on和の公式へのアプローチ 札幌旭丘高等学校 吉田 奏介 1 2 3 l n の場合 まず教科書ではどうだろうか。等差数列の和のところで次のような説明がなされている。 等差数列の和の公式の導入に際し図を用いているが，自然数の和は公式の延長線上としてとら等差数列の和を求める公式の証明 初項がa、公差がdの等差数列において、初項から第n項までの和は、 で求めることができます。今回はこの公式を証明します。 証明 証明の方法を理解するために、まずは具体的な数字の入った数列を例に考えていく。

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

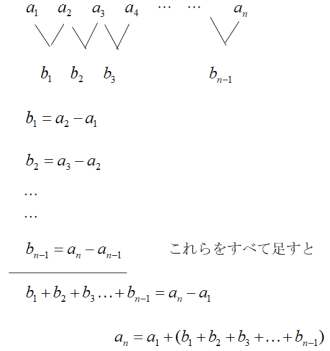
階差数列の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

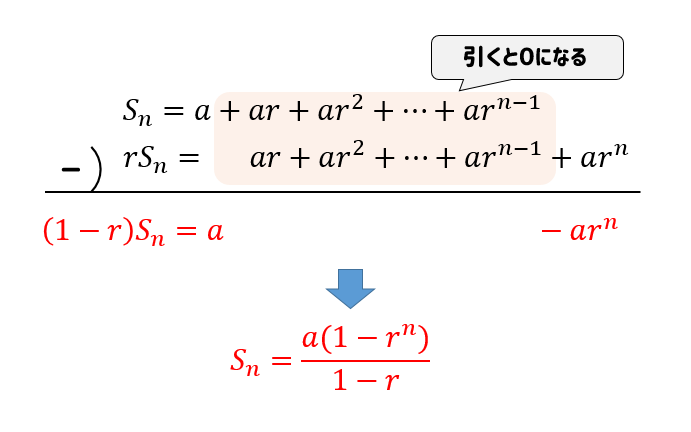
 等差数列・等比数列を分かりやすく考えるコツ 数列の和を求めるとき、式変形をするたびに毎回数列をすべて書いていたら、スペースがいくらあっても足りません。 そのため、多くの場合は総和記号 Σ （シグマ）を使ってまとめて計算することになり であることに注意して，等差数列の和の公式を用いると \begin{align*} \sum_{k=1}^{12n1} z^k & =zz^2z^3\cdots z^{12n1}\\ & =\frac{z(1z^{12n1})}{1z}\\ & =\frac{z(1z)}{1z}\\ &=z \\ & =\cos \frac{\pi}{6} i\sin \frac{\pi}{6}\\ & =\frac{\sqrt{3}}{2}\frac{1}{2}i \end{align*} この実部が求める答えであるから では、次に等比数列の和の公式について説明します。 和の公式を証明！ 等比数列で、初項から第n項までの項をすべて足し合わせると、いくつになるでしょうか？ 実は、和を求めるためにはいちいち足していく必要はなく、 この式に代入すれば求められるのです！ ここではこの、「和の公式」を説明していきます！

Excel エクセルで等差数列の和を計算する方法

いろいろな数列の和 N 2のとき と定義する問題としない問題があります 数学 教えて Goo

 等差数列の和（具体例） 次のような等差数列を考えてみましょう。\ 1,4,7,10,13,16,19 \これは、初項が $1$ で、公差が $3$ 、項数が $7$ の等差数列です。この数列の和を考えてみましょう。 もちろん、前から順番に足していく、という方法もあります。 等差数列公式(其中a1表示第1项,an表示第n项,n表示项数,d表示公差,Sn表示前n项之和) 求末项an=a1(n1)d(a1>an) 求首项a1=an(n1)d(a1>an) 求项数n=(ana1)/d1 求公差d=(ana1)/(d1) 求和Sn=(a1an)*n/2 等差数列の和の公式 等差数列の和の公式とその証明 最後に 等差数列の和の公式 を紹介します。 等差数列の和はそれ自体は公式を覚えることで簡単に用いることができるのですが、応用させた問題が出題されることが多いので正しく理解することが必要

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

3

数列 奇数の和 を求める 大人が学び直す数学

数b等比数列04 等比数列の和の公式証明 Youtube

1

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

これまでで最高の1 から 100 までの和 最高のカラーリングのアイデア

等差数列 等比数列 優技録

等差数列を徹底解説 一般項の求め方や和の公式をマスターしよう Studyplus スタディプラス

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

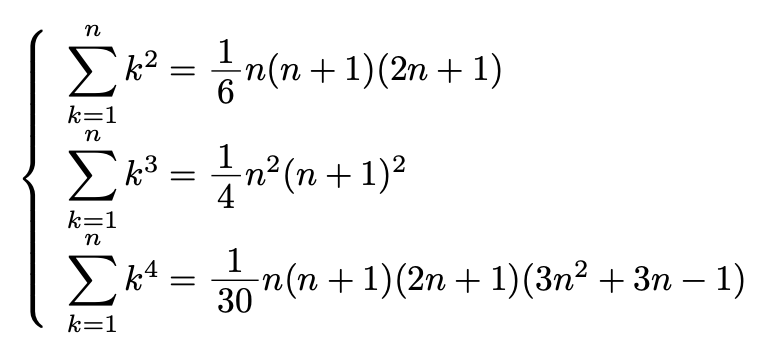
シグマの公式 2乗 3乗 4乗 の証明は 数列の和はこれでマスター 東大医学部生の相談室

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

基本 等差数列の和の公式 初項と公差 数列1 11 Youtube

Q Tbn And9gcsrvyyhjkytc3 8evzp90j3lssnfzqkv5ciallewoxoskrtpciu Usqp Cau

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

数列５ 等差数列の和の公式は不要 ３ 怜悧玲瓏 高校数学を天空から俯瞰する

等比数列

倍数の和 等差数列の利用 大学受験の王道

等差数列について 画像の等差数列の和の公式の証明で 二つの式の 数学 教えて Goo

数列の和の公式 自然数の和 ２s法 Youtube

等差数列の一般項と和 おいしい数学

階差数列

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

等差数列の和を計算する2つの公式 具体例で学ぶ数学

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

高校数学b 等差数列 A N の和 ２ 例題編 映像授業のtry It トライイット

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

等差数列の公式は覚えずに 自分で15秒で作ろう

和の記号s シグマ の公式と 証明方法 高校生向け受験応援メディア 受験のミカタ

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

数学b 等差数列と等比数列 Mike先生のstudyブログ

等差数列を徹底解説 一般項の求め方や和の公式をマスターしよう Studyplus スタディプラス

階差型の数列 おいしい数学

数列の和 小学生でもわかる等差数列の和 東進衛星予備校 名古屋新瑞橋校のブログ

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

問題 次の等差数列の和sを求めよ 100 98 96 Clear

01 等差数列的前n项和公式等差数列的前n项和高中数学 Youtube

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

数列 等差数列の和の公式の証明 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

等差数列の和の公式で 写真のような公式があると思いますが これの Yahoo 知恵袋

至急お願いします 等差数列について 次の和を求めよ 1 3 9 15 Yahoo 知恵袋

数学切り抜き帳

等比数列とは 等比数列の意味と性質 一般項と和の公式をわかりやすく解説 Irohabook

Test 数列公式集 Quizlet

等差数列の性質と一般項と和の公式 等差数列の和は台形の面積 Irohabook

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

階差数列

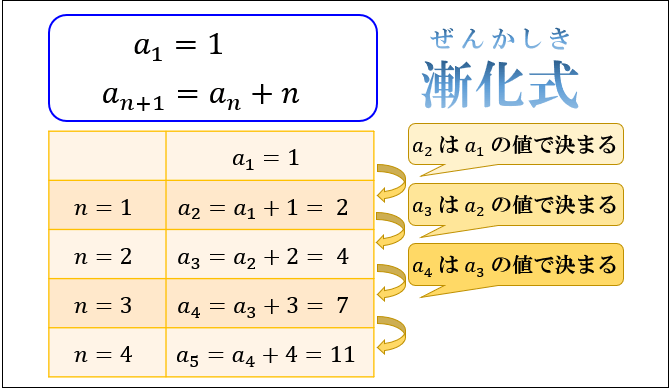
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

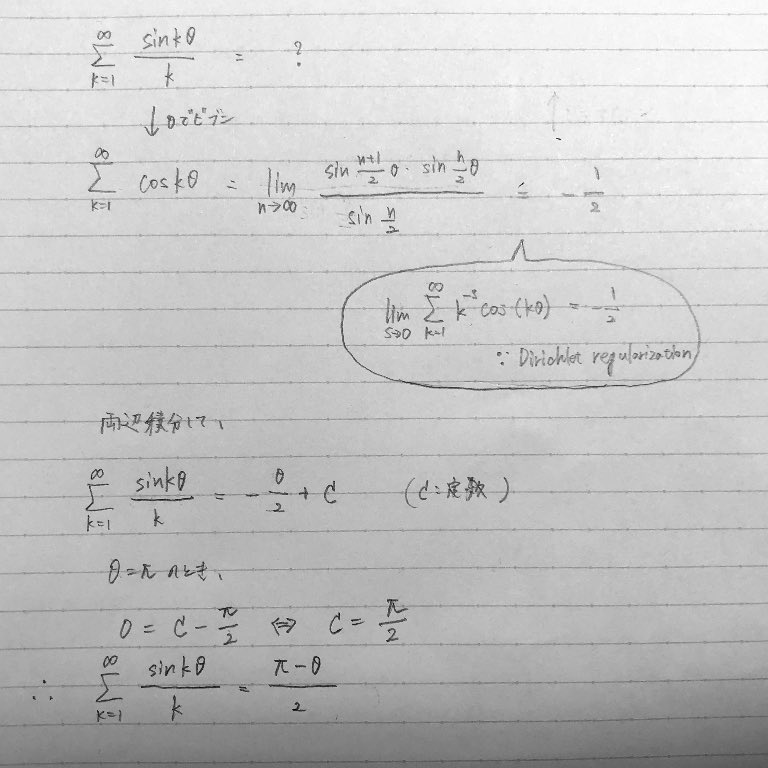
数学を愛する会 位相が等差数列の三角関数の和の公式は マスオさんのサイトを参考にさせて頂きました笑 T Co 0sjxlewsdk

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

数列の基本２ 等差数列の和の公式 と 等比数列の和の公式

数列と級数 Of 京極一樹の数学塾会員頁

48s96ub7b0z5f Net Tousasuuretsunokyoutsuukou

等差数列の和を求める公式の証明 数学b By となりがトトロ マナペディア

高中数学 数列求和方法集锦 含经典例题及解析 转需 知乎

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

等差数列の和の公式の例題と証明など 高校数学の美しい物語

等比数列の一般項と和 おいしい数学

高校数学b 調和数列 逆数が等差数列 の一般項 受験の月

補足 和の公式の証明 高校数学の知識庫

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等比数列 英文

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

階差数列

高校数学b 階差数列から一般項を求める １ 練習編 映像授業のtry It トライイット

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等差数列の和の公式の証明を超分かりやすく解説するよ

数列と級数 Of 京極一樹の数学塾会員頁

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

3

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

48s96ub7b0z5f Net Tousakakerutouhi

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

等差数列の公式 一般項 の証明 数列

等差数列の和の問題について

等差 等比 の和 2次式 等比 の和 おいしい数学

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

高校数学b 等差 等比 型 2次式 等比 型の数列の和 受験の月

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

数列と級数 Of 京極一樹の数学塾会員頁

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

数列と級数 Of 京極一樹の数学塾会員頁

等差数列の一般項や和の公式をマスターしよう ますますmathが好きになる 魔法の数学ノート

高校数学b 数列の和の公式 S公式 Sk の導出 証明 2パターン 受験の月

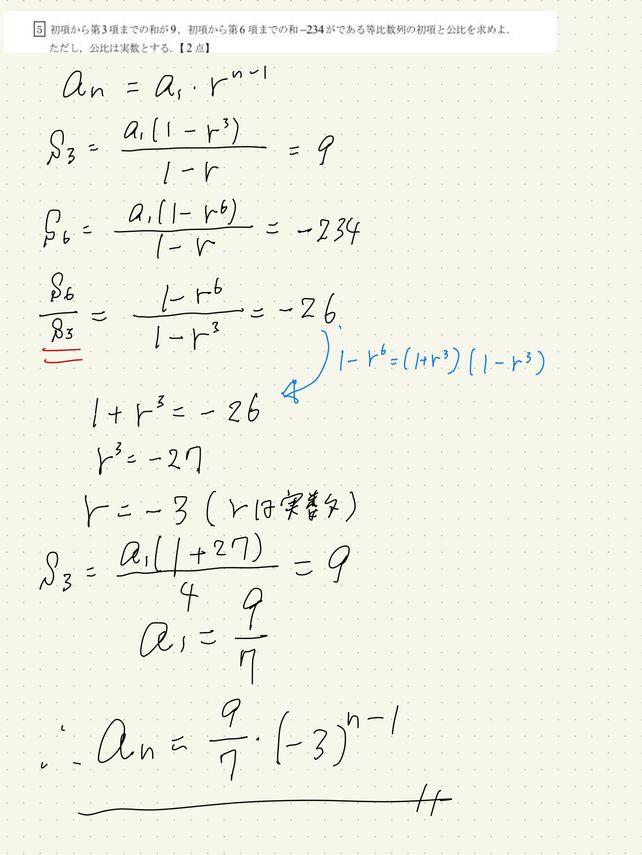
等比数列の和 初項 公比 末項

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

数bの数列の分野での質問です 写真の問13の証明が全くわかりません Clear

等差数列の和 怜悧玲瓏 高校数学を天空から俯瞰する

Incoming Term: 等差数列の和 公式 証明,